Пространственные построения в портретной живописи.
Пространственные построения в портретной живописи.
Автору, конечно, хочется сразу рассказать как использовать находки А. Дюрера, Б. Раушенбаха и труды Г. Гицеску в практике портретирования. Собственно целью этой статьи является обоснование возможности упростить процесс портретирования. То есть, вместо перспективного построения использовать разновидность аксонометрических преобразований методами параллельного переноса.
Тезисно: А. Дюрер, Г. Гицеску, Б. Раушенбах, - вот основа графических построений в портретной живописи.
Из [1] известно, что четвертая книга А. Дюрера содержала:
«… изменения описанных фигур в движении, затем голову, туловище и конечности в перспективе. Применяемый метод состоит в их включении в воображаемые "коробки", находящиеся в перспективе. Этот метод был известен Ломаццо, утверждавшему, что он был изобретен "итальянцем Лукой Канбияри…»
Но,автор на практике, выполняя построение фигур "в воображаемых коробках" в перспективе, постепенно отказался от перспективных преобразований заменив их методами параллельного переноса. Обоснование этой практической находки было найдено в книге Б. Раушенбаха [3]. Но, увы, недавние мои попытки довести до читателя эту науку на художественных форумах показали, что большинство художников не только не читает научную литературу, но и активно отстаивает практику дремучего застоя в развитии индивидуальной техники, яростно обрушиваясь на каждый «новый» для него тезис из очень, очень старых знаний европейского искусства.
Практика непосредственного цитирования предшественников вынуждена - среда, где должны читаться мои статьи по живописи, весьма далека от академической. В академической среде обычно достаточно ссылки на литературу. Поэтому я просто вынужден утомлять читателя цитированием, чтобы у него не возник соблазн слушать гипнотизирующий блеф «гросс - искусствоведов».
Прежде всего процитирую (все цитаты выделены) книгу Н. В. Четверухина [5], чтобы ввести единую систему терминов. Прошу отметить, что исследования по начертательной геометрии финансировались в рамках развития технического черчения, поэтому вместо термина «рисунок» применяется термин «чертеж». Автор несколько отредактировал рисунки и условные обозначения, чтобы они были воспринимаемы стандартным текстовым редактором. Также на рисунке b13-1 и далее заменены изображения лучей на изображения прямых, как в тексте цитируемой книги, перемещена картинная плоскость и т.п.
… Наиболее существенными из этих требований являются следующие:
1. Чертеж должен быть наглядным, т. е. он должен вызывать пространственное
представление изображаемого предмета.
2. Он должен быть обратимым , т. е. таким, чтобы по нему можно было бы точно воспроизвести форму и
размеры изображаемого предмета.
3. Чертеж должен быть достаточно простым с точки зрения его графического выполнения.
4. Графические операции, выполняемые на чертеже, должны давать достаточно точные решения.
Проанализируем более подробно требование «обратимости» чертежа. Для всех видов технических чертежей это требование является особенно важным. Чертеж есть производственный документ, по которому выполняется то или другое изделие. Поэтому необходимо, чтобы по чертежу можно было точно установить форму и размеры будущего изделия, а также некоторые другие данные о нем. Кроме того, чертеж дает наглядное представление об изделии, что в свою очередь облегчает его выполнение. Никакие описания предмета не могут заменить чертежа. Последний является «языком техника», как говорил один из создателей начертательной геометрии французский ученый и инженер Гаспар Монж (1746—1818).
Легко понять, что не всякое изображение предмета на листе бумаги позволяет точно определить его геометрическую фигуру. Для этого необходимо, чтобы изображение (чертеж) предмета было построено по определенным геометрическим правилам, позволяющим от плоских и, следовательно, искаженных форм на чертеже переходить к натуральным пространственным формам изображаемого предмета. Такое геометрически закономерное изображение пространственного предмета на плоскости достигается при помощи метода
проектирования (От латинского слова ргojеcere — ,бросать вперед, бросаться в глаза), который является основным методом в начертательной геометрии. Чертежи, построенные по методу проектирования, получили название проекционных . Следует иметь в виду, что переход от пространственных предметов, непосредственно наблюдаемых учащимися, к их изображениям на плоскости (проекционным чертежам), а затем умение пользоваться такими изображениями взамен самих предметов нередко вызывают на первых порах большие трудности у учащихся. Эти трудности происходят от недостаточного развития у некоторых из них пространственных представлений и пространственного воображения. Начертательная геометрия является той научной дисциплиной, которая помогает развитию пространственных представлений, необходимых не только в технике, но и вообще в практической жизни человека. На первых порах изучения начертательной геометрии полезно обращаться к моделированию соответствующих геометрических форм. В дальнейшем задача преподавания заключается в том. чтобы учащиеся привыкли выполнять операции над пространственными фигурами на их проекционных изображениях, не прибегая к помощи моделей. Это не означает, что в отдельных сложных задачах, трудных для представлений учащихся, нельзя прибегать к помощи моделирования.
§ 1. Метод проектирования пространственной фигуры на плоскость.
1. Центральна я проекция (перспектива, от латинского слова projecere — бросать вперед)*. Пусть имеем в пространстве плоскость P, которую будем называть плоскостью проекций , или «картинной» плоскостью (рис. b13-1). Выберем какую-либо точку S, не лежащую на плоскости проекций. Эту точку будем называть центром проектирования , или «глазом».
Чтобы спроектировать точку A пространства на плоскость P, проводим через данную точку A и центр проекций S прямую.
Такая прямая носит название проектирующей прямой . Находим затем точку пересечения проектирующей прямой SA с плоскостью проекций P. Полученную точку пересечения А' и будем называть центральной проекцией данной точки А на плоскость Р.
Заметим, что описанным способом не может быть построена проекция точки A в том случае, когда она совпадает с центром проекций S. В самом деле, в этом случае становится неопределенной не только проектирующая прямая, но и проекция точки на плоскости P. Таким образом, центр проекций S является исключительной точкой, не имеющей проекции
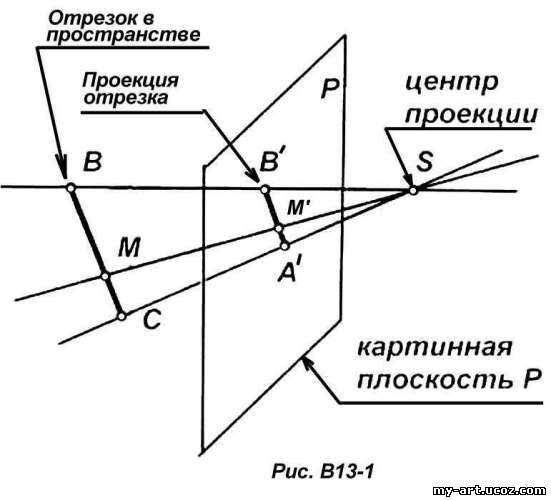
…Однако, как было ранее упомянуто, на практике большое значение имеют также другие качества проекционных чертежей, в частности простота построения и возможность воспроизведения формы и размеров изображаемого предмета, т. е. обратимость чертежей. В этом отношении перспективные чертежи не являются наиболее удобными. Поэтому наряду с центральным проектированием большим распространением пользуется также способ параллельного проектирования для построения изображений пространственных фигур.
2. Параллельная проекция. Как и в описанном случае, задаем некоторую плоскость ГГ, являющуюся плоскостью проекций, или «картинной» плоскостью. Кроме того, задаем направление проектирования S, непараллельное плоскости проекции P (b13-4рис. 3). Самая операция проектирования выполняется следующим образом. Чтобы спроектировать какую-либо точку А пространства, проводим через нее проектирующую прямую АА параллельную направлению проектирования (Разумеется, как и в случае центральной проекции, исключением является проектирующая прямая, проекция которой сводится к одной точке.).
2. Параллельная проекция. Как и в описанном случае, задаем некоторую плоскость ГГ, являющуюся плоскостью проекций, или «картинной» плоскостью. Кроме того, задаем направление проектирования S, непараллельное плоскости проекции P (b13-4рис. 3). Самая операция проектирования выполняется следующим образом. Чтобы спроектировать какую-либо точку А пространства, проводим через нее проектирующую прямую АА параллельную направлению проектирования (Разумеется, как и в случае центральной проекции, исключением является проектирующая прямая, проекция которой сводится к одной точке.).

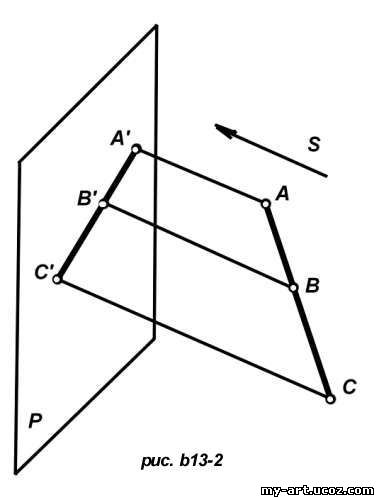
Точка пересечения А' проектирующей прямой с плоскостью P и является параллельной проекцией точки A на плоскость P. Сохраняя то определение проекции фигуры, которое было дано в случае центральной проекции, мы придем к выводу, что параллельной проекцией прямой линии является прямая.
Так, на рис. b13-2 изображена операция параллельного проектирования отрезка АВ. Проектирующие линии всех точек этого отрезка лежат в одной (проектирующей) плоскости. Поэтому проекцией отрезка АВ является отрезок А'В' прямой линии. Остановимся на некоторых свойствах параллельной проекции. Как мы уже видели, параллельной проекцией прямой линии является прямая. Таким образом, это свойство центральной проекции сохраняется и при параллельном проектировании. Вместе с тем параллельная проекция обладает еще другими свойствами, которых не имеет центральная проекция. К ним относятся следующие: Действительно, пусть имеем прямые AB и CD, параллельные в пространстве (рис. b13-3).
Так, на рис. b13-2 изображена операция параллельного проектирования отрезка АВ. Проектирующие линии всех точек этого отрезка лежат в одной (проектирующей) плоскости. Поэтому проекцией отрезка АВ является отрезок А'В' прямой линии. Остановимся на некоторых свойствах параллельной проекции. Как мы уже видели, параллельной проекцией прямой линии является прямая. Таким образом, это свойство центральной проекции сохраняется и при параллельном проектировании. Вместе с тем параллельная проекция обладает еще другими свойствами, которых не имеет центральная проекция. К ним относятся следующие: Действительно, пусть имеем прямые AB и CD, параллельные в пространстве (рис. b13-3).
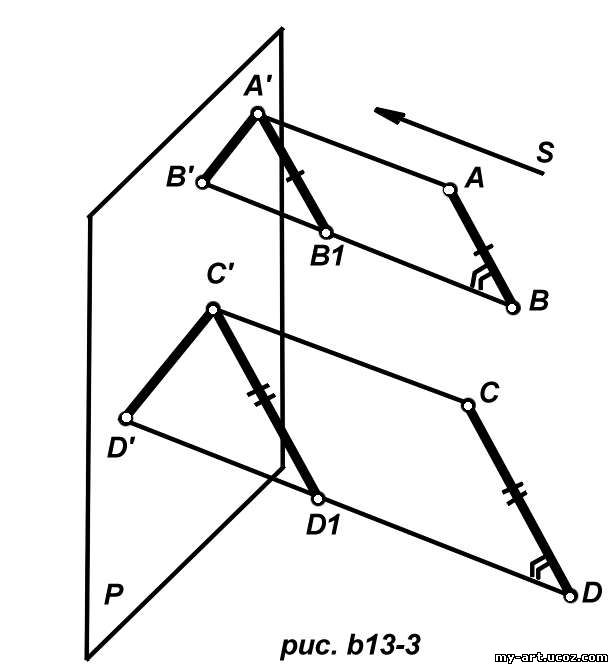
Прямые, параллельные в пространстве (в общем случае), проектируются в виде прямых, параллельных на плоскости проекций P . Построив для них проектирующие плоскости AA'B'B и CC'D'D, заметим, что эти плоскости параллельны как плоскости, имеющие углы с соответственно параллельными сторонами
(AB||CD; BB||DD').
Поэтому проектирующие плоскости пересекают плоскость проекций P по двум параллельным между собой прямым.
2.2 Отношение отрезков, лежащих на параллельных прямых или на одной прямой), сохраняется в параллельной проекции .
Пусть AB и CD — отрезки, лежащие на параллельных прямых. Построим их проекции на плоскость P при направлении, проектирования S (см. рис. B13-3).
Проведем в проектирующих плоскостях отрезки A'B1 и C'D1, соответственно параллельные и равные отрезкам AB и CD. Тогда, очевидно, треугольники A'B'B» и C'D'D являются подобными, так как их соответственные стороны параллельны. Отсюда заключаем, что
AB/CD = AА'B1/C'D1 =A'B'/C'D'
В частном случае данные отрезки АВ и СО могут оказаться лежащими на одной прямой, однако это не изменит рассуждения. Если при этом концы двух отрезков совпадают, т. е. мы имеем отрезки АВ и ВС (рис. b13-2), то указанное соотношение примет следующий вид:
AB / BC=A'B' / B'C'
Отсюда следует, что отношение, в котором точка В делит отрезок АС, сохраняется в проекции для точки В', делящей отрезок А'С'. В частности, середина натурального отрезка проектируется серединой отрезка-проекции.
2.3 Центр тяжести треугольной пластинки (как точка пересечения медиан) проектируется в виде центра тяжести треугольника-проекции.
2.5 Окружность как центральносимметричная кривая, все диаметры которой делятся в центре пополам, проектируется в виде центральносимметричной кривой (эллипс), все диаметры которой также делятся в центре пополам. 2.6. Отношение проекции отрезка А'В' к натуральному отрезку постоянно для всех параллельных между собой отрезко . Действительно, полученная выше пропорция:
AB / CD=A'B' / C' D'
после перестановки крайних членов может быть написана так:
A'B'/ AB= C'D'/ CD
Постоянное отношение и называется показателем искажения для отрезков данного направления.
3. Ортогональная проекция. Параллельная проекция называется ортогональной (прямоугольной), если направление проектирования S перпендикулярно к плоскости проекций P.
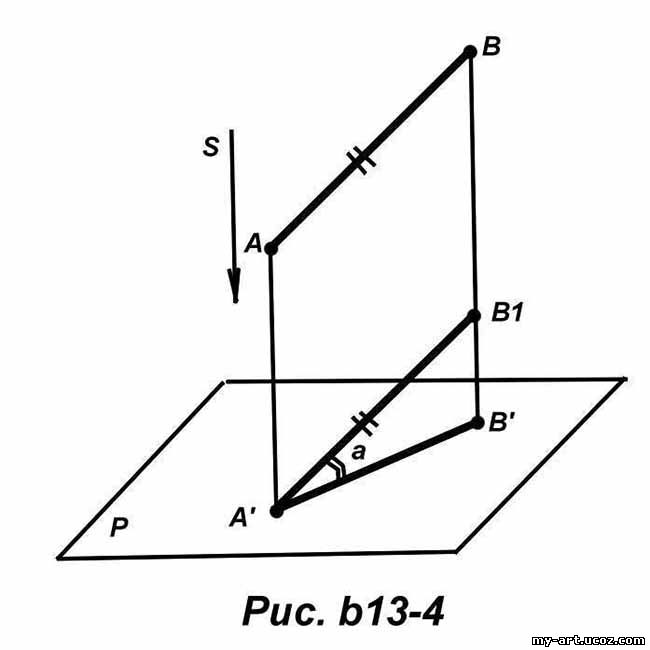
В ортогональной проекции очень просто устанавливать соотношение между длиной натурального отрезка и длиной его проекции. Предположим, что отрезок АВ образует с плоскостью проекций P прямой угол (рис. b13-4).
(AB||CD; BB||DD').
Поэтому проектирующие плоскости пересекают плоскость проекций P по двум параллельным между собой прямым.
2.2 Отношение отрезков, лежащих на параллельных прямых или на одной прямой), сохраняется в параллельной проекции .
Пусть AB и CD — отрезки, лежащие на параллельных прямых. Построим их проекции на плоскость P при направлении, проектирования S (см. рис. B13-3).
Проведем в проектирующих плоскостях отрезки A'B1 и C'D1, соответственно параллельные и равные отрезкам AB и CD. Тогда, очевидно, треугольники A'B'B» и C'D'D являются подобными, так как их соответственные стороны параллельны. Отсюда заключаем, что
AB/CD = AА'B1/C'D1 =A'B'/C'D'
В частном случае данные отрезки АВ и СО могут оказаться лежащими на одной прямой, однако это не изменит рассуждения. Если при этом концы двух отрезков совпадают, т. е. мы имеем отрезки АВ и ВС (рис. b13-2), то указанное соотношение примет следующий вид:
AB / BC=A'B' / B'C'
Отсюда следует, что отношение, в котором точка В делит отрезок АС, сохраняется в проекции для точки В', делящей отрезок А'С'. В частности, середина натурального отрезка проектируется серединой отрезка-проекции.
2.3 Центр тяжести треугольной пластинки (как точка пересечения медиан) проектируется в виде центра тяжести треугольника-проекции.
2.5 Окружность как центральносимметричная кривая, все диаметры которой делятся в центре пополам, проектируется в виде центральносимметричной кривой (эллипс), все диаметры которой также делятся в центре пополам. 2.6. Отношение проекции отрезка А'В' к натуральному отрезку постоянно для всех параллельных между собой отрезко . Действительно, полученная выше пропорция:
AB / CD=A'B' / C' D'
после перестановки крайних членов может быть написана так:
A'B'/ AB= C'D'/ CD
Постоянное отношение и называется показателем искажения для отрезков данного направления.
3. Ортогональная проекция. Параллельная проекция называется ортогональной (прямоугольной), если направление проектирования S перпендикулярно к плоскости проекций P.
В ортогональной проекции очень просто устанавливать соотношение между длиной натурального отрезка и длиной его проекции. Предположим, что отрезок АВ образует с плоскостью проекций P прямой угол (рис. b13-4).

проведем А'В параллельно АВ. Тогда будем иметь: A'B'=AВ cos (a) где через (a обозначен угол отрезка AB к плоскости проекций P. (Доказательство этой формулы приведено в школьных учебниках по стереометрии.)
Как видно из описания свойств центральной, параллельной и ортогональной проекций, первая, обладая большей наглядностью, вместе с тем в значительной степени искажает натуральную форму и размеры фигуры. Вторая (т. е. параллельная) проекция сохраняет некоторые свойства натуральной фигуры (параллельность прямых линий, отношение отрезков), но не обладает, однако, той степенью наглядности, которая свойственна центральной проекции. Последнее обстоятельство особенно заметно при изображении объектов большой протяженности, например, зданий, мостов и др.
Параллельная проекция, однако, является весьма удобной при изображении объектов относительно небольших размеров, например узлов и деталей в машиностроении.
В частности, большое распространение в технических чертежах получила ортогональная проекция, позволяющая особенно легко судить о размерах изображаемых предметов. Что же касается центральной проекции, или перспективы, то она применима главным образом в архитектурно-строительных чертежах.
В заключении этой цитаты отмечу, что в природе точек, линий прямых углов, криволинейных контуров и линий проходящих через глаз нет. Это производное от механизма восприятия. Эти объекты воспринимают зрительные рецепторы и механизмы обработки информации глаза человека. Подробнее в [4].
Теперь перспективное проектирование рассмотрим с другой стороны.
Так – ли глаз видит.
Перспективное проектирование не способ видения мира глазом человека. Закон иллюзии константности формы, разные механизмы восприятия центрального поля зрения и периферийного при восприятии определяет другую - перцептивную проекцию проекцию как способ восприятия.
Поэтому приведу пространную цитату из книги [3] доказывающую допустимость построений портретов методами параллельного переноса.
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ О ЗРИТЕЛЬНОМ ВОСПРИЯТИИ.
Если схематизировать процесс зрительного восприятия, то простейшая его модель говорит о том, что оно является двухступенчатым. Первой ступенью является образование изображения внешнего пространства на сетчатке глаза, а второй - воссоздание на этой основе облика внешнего пространства в человеческом сознании. О том, что эти две ступени качественно различны, говорит хотя бы тот геометрический факт, что изображение на сетчатке глаза является двумерным (в первом приближении плоским, наподобие картины), в то время как образованное на этой основе представление о внешнем пространстве - трехмерным, объемным. Образование двумерного изображения на сетчатке глаза - процесс в достаточной степени известный и в своей основе аналогичный возникновению изображения на фотопленке с помощью объектива фотоаппарата. Правда, здесь имеют место психофизиологически существенные отличия. Глаз находится в непрерывном движении, "осматривая" внешнее пространство сравнительно узким лучом зрения, и исследования этого подсознательного движения показывают его исключительное значение в процессе зрительного восприятия.
"Однако, поскольку ниже по сути рассматриваемых вопросов наиболее важным является вопрос о геометрических свойствах изображения, образовавшегося на сетчатке глаза, всюду будет приниматься простейшая модель, согласно которой на сетчатке в достаточно большом угле зрения двумерное изображение внешнего мира получается путем его проектирования при помощи хрусталика, выполняющего роль, аналогичную роли объектива фотоаппарата. Такое изображение на сетчатке глаза называют ретинальным изображением (от слова ретина - сетчатка глаза) или сетчаточным образом. Полезно еще раз подчеркнуть, что используемое здесь и ниже понятие "сетчаточный образ" является в достаточной мере условным: оно не учитывает фактической вогнутости поверхности сетчатки и подвижности глаза. Помимо того, сама сетчатка не является однородной - центральная (фовеальная) часть сетчатки дает наилучшее восприятие деталей и цветов, в то время как периферическая ее часть дает малую четкость восприятия. Следовательно, используемое в книге понятие "сетчаточный образ" является некоторой идеализацией, учитывающей совокупный эффект первой ступени зрительного восприятия. Сетчаточный образ дает сильно искаженную картину внешнего мира. Эти искажения прежде всего связаны с тем. что близкие предметы будут казаться огромными, а более удаленные - маленькими.
Ретинальное изображение само по себе не содержит никакой информации о расстояниях до предметов, образы которых возникли на сетчатке глаза. Поэтому соответствующее дополнение сетчаточного образа возможно путем привлечения какой-то другой информации. Этот процесс ввода дополнительной информации и является второй ступенью зрительного восприятия. Нужная информация извлекается из "запасов памяти" человеческого мозга. Несколько упрощая картину, можно утверждать, что человеческое сознание хранит в своей памяти опыт предшествующей жизни начиная с первых дней младенчества и даже генетически передаваемый опыт пред- шествующих поколений. Пользуясь этим опытом, человеческое сознание воссоздает по сетчаточному образу истинную картину внешнего мира с раз- умной степенью точности. Для последующего важно отметить, что образ внешнего мира, создаваемый мозгом, не является точной копией реального внешнего мира. Эта точность биологически бессмысленна и даже вредна - точным должно быть восприятие близких областей пространства, областей, могущих таить в себе опасность или могущих служить для добывания пищи, в то время как удаленные области можно и даже разумно воспринимать менее подробно и точно (чтобы не перегружать мозг излишней информацией, несущественной для определения поведения).
Эти "запасы памяти" являются не чем иным, как полученным в результате активной человеческой деятельности опытом, который позволяет с известным приближением правильно воспринимать окружающий человека объективный мир, давать хотя и приближенное, но адекватное отображение его, в сознании человека. Опыт познания внешнего мира, о котором здесь идет речь, не является суммой или итогом накопленной зрительной информации. Он включает всю совокупную человеческую практическую деятельность, которая позволяет корректировать представления человека о внешнем мире, коррелировать эти представления со зрительным восприятием и создавать, в конце концов, адекватный зрительный образ окружающего человека объективного мира с нужной степенью подробности и точности.
Воссоздаваемая мозгом по сетчаточному образу картина внешнего мира приобретает вид трехмерного пространства, но, как уже говорилось, иного по сравнений с реальным трехмерным, пространством. Поскольку художник в случае, когда целью его творчества является рисунок, а не чертеж, дол- жен уметь изображать именно зрительно воспринимаемое (перцептивное) пространство, его свойства следует рассмотреть более подробно. Если ограничиться только геометрией, то проблема сводится к вопросу о том, каким образом двумерное ретинальное изображение трансформируется в трехмерное перцептивное, точнее, каким геометрическим законам это преобразование подчиняется.
Прежде всего (не во времени, конечно, а логически) следует мысленно распределить все полученные на сетчатке изображения на соответствующие расстоянию от созерцающего их человека. Это распределение в направлениях "близко-далеко” происходит подсознательно, на основе предшествующего опыта, причем человек подсознательно пользуется рядом признаков глубины видимого пространства. Эти признаки можно условно разбить на две группы - монокулярные и бинокулярные. Первая группа характеризуется тем, что включенные в нее признаки глубины действуют и тогда, когда человек смотрит одним глазом.
К монокулярным признакам глубины можно отнести следующие:
1) перекрытие - более близкие предметы могут заслонять собой более далекие;
2) уменьшение размеров предметов по мере их удаления от зрителя; особенно эффективен этот признак, если рассматриваются предметы, истинный размер которых известен (деревья и т. п.);
3) явление воздушной перспективы - далекие предметы видны менее четко и меняют свой цвет (наблюдаются как бы через голубоватую дымку); 4) далекие предметы видны сдвинутыми вверх в поле зрения, точнее, приближенными к горизонту;
5) большие предметы (круглые крепостные башни, большие здания и т. п.), освещенные солнцем, оказываются затененными различным образом в различных своих частях, и наблюдаемая система теней способна дать представление о более близких и более далеких частях этих предметов; особенно эффективен этот признак для больших криволинейных и ребристых поверхностей.
Здесь перечислены не все монокулярные признаки глубины, но основные, причем те, которые будут нужны ниже.
К бинокулярным признакам глубины следует отнести:
1) конвергенцию - поворот оптических осей глаз в направлении рассматриваемого предмета, обычно (при взгляде вдаль) оптические оси глаз параллельны, однако если рассматривать достаточно близкий предмет, то соответствующие мышцы сводят оптические оси глаз так, чтобы они пересеклись в разглядываемой области пространства, и соответствующие мышечные усилия сигнализируют о близости или удаленности предмета;
2) диспаратность - даже если и не рассматривать какой-то предмет, то в силу того, что глаза разнесены, изображение, полученное левым и правым глазом, оказывается различным, причем тем более различным, чем ближе предметы к смотрящему.
Признаки глубины, действуя в совокупности, позволяют подучить достаточно полное представление о расстояниях до различных предметов причем по мере приближения к смотрящему число и "точность показаний признаков увеличиваются в полном соответствии с биологической потребностью человека. Если для больших расстояний нужная информация о дистанциях до предметов дается первыми четырьмя монокулярными признаками, то в непосредственной близости от человека действуют бинокулярные признаки и все монокулярные, за исключением лишь явления воздушной перспективы. Вдумчивое рассмотрение всех приведенных признаков глубины показывает, что они не могут быть непосредственно получены из сетчаточного образа, а рождены предшествующим опытом.
Даже такой, казалось бы, безусловный признак, как заслонение близких предметом далекого, не абсолютен, он предполагает знание истинной форм [2] частично заслоненного предмета, ибо иначе невозможно решить, являете .ли его видимая часть полной (а следовательно, не заслоненной) формой Таким образом, человеческий мозг, используя накопленный предшествующий опыт, дает принципиальную возможность построить по двумерном сетчаточному образу трехмерное перцептивное пространство.
Помимо подсознательного анализа зрительной информации, возникновению пространственного образа в сознании человека способствует информация (тоже извлекаемая из запасов памяти), никак не связанная со зрением. Находясь в привычном мире, человек не только созерцает его, но непрерывно взаимодействует с ним в своей практической деятельности: он перемещается, берет предметы в руки и т. п. Поэтому он прекрасно знает их размеры, форму своей комнаты, своего письменного стола, лежащих на нем предметов и вообще геометрические свойства окружающего его мира. То, что это знание может быть никак непосредственно не связанным со зрением (хотя весьма и помогающим ему), показывает практическая деятельность слепых. Слепой безошибочно находит нужные ему предметы в своей комнате, быстро и без посторонней помощи ходит по своей квартире и т. д. Это знание пространства, его размеров и формы можно назвать осязательно - кинестетичским представлением о нем, в частности позволяющим знать удаления в нем предметов от человека.
Хотя и в несколько иной форме, и возможно несколько ослаблено, это знание присуще и зрячему. В последнем нетрудно убедиться, разглядывая близкие предметы сначала двумя глазами, а затем закрыв один глаз. Казалось бы, "отключение” столь важных на малых расстояниях бинокулярны признаков глубины должно было бы вызвать существенное изменение зрительного восприятия. Однако ничего подобного не происходив человек продолжает видеть предметы в целом такими же и, главное, пространственными. Место бинокулярных признаков глубины в этом случае занимают осязательно-кинестетические представления. Таким образом, бинокулярные признаки глубины и осязательно-кинестетические представления выступают как бы в некотором единстве, способствуя правильной и точной оценки расстояний до предметов.
В том случае, когда искусственным образом у человека одновременно "отключались” оба названных источника информации, т. е. когда при наблюдении одним глазом из должным образом выбранной точки ему предъявлялись пространственные конструкции неизвестных ему и непривычных форм, оказалось возможным вызвать у человека зрительные иллюзии, совершенно искажающие фактические пространственные отношения. Об этом, в частности, говорят известные опыты с "перекошенной комнатой” Эймса Таким образом, признаки глубины, которыми способен пользоваться человек для "размещения” зафиксированных в сетчаточном образе предметов в направлении "близко-далеко”, сводятся к монокулярным и бинокулярным, дополненным осязательно-кинестетическими представлениями. Эффективность действия осязательно-кинестетических представлений, как и бинокулярных признаков глубины, падает с увеличением расстояния до созерцаемых предметов, если иметь в виду превышение расстояний, ограничивающих несколько неопределенную границу "непосредственного окружения” человека. Большие расстояния не столь важны биологически, и поэтому излишняя перегрузка памяти детальной информацией о больших областях пространства была бы биологически неразумна.
Возвращаясь к вопросу о формировании в человеческом сознании перцептивного пространства, отметим почти очевидное обстоятельство: одного "размещения” зарегистрированных сетчаткой глаза предметов по некоторой шкале расстояний недостаточно. Оптические процессы, связанные с работой глаза, дают на сетчатке явно искаженную картину внешнего мира - близкие предметы получаются большими, а далекие маленькими, даже если в объективном внешнем пространстве они совершенно одинаковы. С подобного рода искажением можно мириться для далеких областей пространства, однако для близких, имеющих первостепенную биологическую важность, всякого рода искажения крайне нежелательны, так как они могут привести к ошибкам поведения. Поэтому одной из задач системы зрительного восприятия является переработка в процессе второй ступени восприятия геометрических соотношений сетчаточного образа, причем эта переработка сильнее, чем ближе созерцаемая область пространства. Эти процессы "исправления” геометрии сетчаточного образа в настоящее время достаточно хорошо изучены и получили в психологии зрительного восприятия наименование механизмов константности. Остановимся на двух таких механизмах - механизме константности величины и механизме константности формы (другие механизмы константности, например константности цвета, как не имеющие геометрической природы, рассматриваться не будут).
Механизм константности величины связан с компенсацией уменьшения изображения некоторого предмета на сетчатке по мере его удаления. В зоне непосредственного окружения человека (т. е. в радиусе единиц метров) эта компенсация является почти полной. Следовательно, зрительный образ близкого предмета, возникающий в нашем сознании, может сильно отличаться по относительной величине от соответствующего ему сетчаточного образа, но зато будет согласован с истинной величиной созерцаемого предмета. В сказанном легко убедиться, рассматривая, например, пол в небольшой комнате. Действительно, наблюдая доски пола или паркетные полосы на расстоянии 3-4 м от себя и у своих ног, почти не ощущаешь их видимого ( См., например: ) сужения, в то время как на сетчатке глаза соответствующее сужение будет примерно двукратным (в согласии с отношением названного выше раccтояния к росту человека).
Таким образом, хотя по мере увеличения расстояния до объекта его величина на сетчатке уменьшается пропорционально расстоянию, воспринимаемая величина остается почти неизменной, константной (отсюда и название этого закона восприятия - механизм константности величины). Указанный факт хорошо известен художникам-портретистам. Создавая групповой портрет, художник пишет головы всех изображаемых приблизительно одинаковой величины, хотя на сетчатке глаза художника голова расположенного близко человека может быть много больше головы расположенного в глубине группы. Механизм константности величины не только увеличивает размеры удаленных предметов, но и уменьшает размеры слишком близких, например ладони, поднесенной к глазу. Как показали опыты, свойство константности величины оказывается почти абсолютным, настолько точно человеческое сознание воссоздает истинные размеры предметов по сетчаточному образу, если оно имеет информацию о расстояниях до них, однако при этом обнаружилось два фактора, которые неизменно снижали или полностью исключали действие механизма констант- ности величины:
1) константность нарушалась по отношению к далеким предметам;
2) константность не сохранялась и для близких предметов, если эти предметы имели мало или не имели вовсе признаков глубины
4. Оба эти экспериментальных факта полностью согласуются с нарисованной выше теоретической картиной - информация о далеких предметах имеет второстепенную биологическую ценность, а образование трехмерного перцептивного пространства возможно лишь при использовании признаков глубины, не содержащихся непосредственно в ретинальных изображениях. Механизм константности формы имеет аналогичную природу, однако касается формы предметов представим себе, что человек смотрит на пред- меты, имеющие простую форму - круга, квадрата и т. п. (например, по- верхности круглого или квадратного стола). Если смотреть на эти предметы под некоторым произвольным углом, то круг будет восприниматься как овал, квадрат - как фигура, похожая на ромб, и т. д. Действие механизма константности формы сказывается в том, что если человек заранее знает истинную форму созерцаемых предметов из своего предшествующего опыта, то круглые предметы кажутся ему не столь овальными, как их ретинальные изображения; углы ромбов оказываются более близкими к 90°, чем у их изо- бражений на сетчатке глаза (т. е. приближенными к квадрату), и т. д. Человеческое сознание стремится компенсировать не только искажения относительных размеров, но и искаженную форму предметов, возникающую при проектировании этих предметов на сетчатку при помощи оптической системы глаза. Хорошо известно, например, что экран телевизора можно наблюдать "сбоку” с большим отклонением от направления, перпендикулярного к плоскости экрана, и тем не менее видимая форма экрана будет сохраняться в виде вытянутого по горизонтали прямоугольника привычных очертаний, хотя на сетчатке его изображение уже может стать квадратным или даже вытянутым по вертикали. Механизм константности формы сравнительно легко изучить количественно, ставя опыты с предметами простой формы (круг, квадрат и т. п.), однако это не значит, что он не действует на сетчаточные изображения более сложных объектов.
Относительно эффективности механизма константности формы надо заметить следующее: 1) как уже говорилось, его действие тем сильнее, чем лучше известна {заранее, из предыдущего опыта) форма созерцаемого предмета;
2) он действует лишь на сравнительно малых расстояниях и совершенно .не эффективен для предметов, достаточно удаленных от смотрящего. Разумность обоих приведенных здесь условий с биологической точки зрения достаточно очевидна.
Возвращаясь к вопросу о двуступенчатом характере зрительного восприятия человека (в той степени подробности, которая нужна для последу- ющего), можно утверждать, что первой ступенью является образование на сетчатке изображения внешнего мира при помощи оптической системы глаза, а второй - воссоздание на этой основе трехмерного перцептивного про- странства с подсознательным использованием признаков глубины и осязательно-кинестетических представлений путем преобразования сетчаточного образа механизмами константности величины и формы. Последние как бы "растягивают” и "сжимают” отдельные элементы сетчаточного образа, подвергая наиболее существенным преобразованиям имеющую первостепенную биологическую важность часть сетчаточного образа, соответствующую области непосредственного окружения человека.
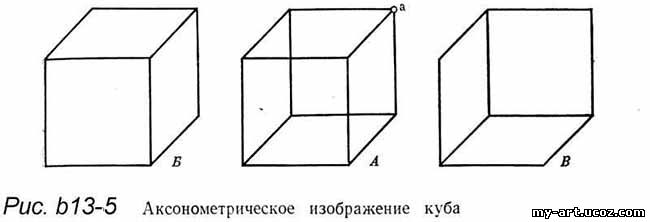
Сказанное здесь может создать излишне упрощенное представление о работе мозга при зрительном восприятии. Чтобы несколько уточнить характер работы мозга (опять лишь в той степени, в которой это будет нужно для последующего) и проиллюстрировать некоторые приводившиеся выше утверждения, обратимся к следующему примеру. На рис. b13-5 в средней части рисунка изображен куб, причем использована так называемая аксонометрическая проекция, при которой в изображении сохраняется свойство параллельности (ребра, параллельные у реального куба, изображены прямыми, которые между собой параллельны).
Как видно из описания свойств центральной, параллельной и ортогональной проекций, первая, обладая большей наглядностью, вместе с тем в значительной степени искажает натуральную форму и размеры фигуры. Вторая (т. е. параллельная) проекция сохраняет некоторые свойства натуральной фигуры (параллельность прямых линий, отношение отрезков), но не обладает, однако, той степенью наглядности, которая свойственна центральной проекции. Последнее обстоятельство особенно заметно при изображении объектов большой протяженности, например, зданий, мостов и др.
Параллельная проекция, однако, является весьма удобной при изображении объектов относительно небольших размеров, например узлов и деталей в машиностроении.
В частности, большое распространение в технических чертежах получила ортогональная проекция, позволяющая особенно легко судить о размерах изображаемых предметов. Что же касается центральной проекции, или перспективы, то она применима главным образом в архитектурно-строительных чертежах.
В заключении этой цитаты отмечу, что в природе точек, линий прямых углов, криволинейных контуров и линий проходящих через глаз нет. Это производное от механизма восприятия. Эти объекты воспринимают зрительные рецепторы и механизмы обработки информации глаза человека. Подробнее в [4].
Теперь перспективное проектирование рассмотрим с другой стороны.
Так – ли глаз видит.
Перспективное проектирование не способ видения мира глазом человека. Закон иллюзии константности формы, разные механизмы восприятия центрального поля зрения и периферийного при восприятии определяет другую - перцептивную проекцию проекцию как способ восприятия.
Поэтому приведу пространную цитату из книги [3] доказывающую допустимость построений портретов методами параллельного переноса.
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ О ЗРИТЕЛЬНОМ ВОСПРИЯТИИ.
Если схематизировать процесс зрительного восприятия, то простейшая его модель говорит о том, что оно является двухступенчатым. Первой ступенью является образование изображения внешнего пространства на сетчатке глаза, а второй - воссоздание на этой основе облика внешнего пространства в человеческом сознании. О том, что эти две ступени качественно различны, говорит хотя бы тот геометрический факт, что изображение на сетчатке глаза является двумерным (в первом приближении плоским, наподобие картины), в то время как образованное на этой основе представление о внешнем пространстве - трехмерным, объемным. Образование двумерного изображения на сетчатке глаза - процесс в достаточной степени известный и в своей основе аналогичный возникновению изображения на фотопленке с помощью объектива фотоаппарата. Правда, здесь имеют место психофизиологически существенные отличия. Глаз находится в непрерывном движении, "осматривая" внешнее пространство сравнительно узким лучом зрения, и исследования этого подсознательного движения показывают его исключительное значение в процессе зрительного восприятия.
"Однако, поскольку ниже по сути рассматриваемых вопросов наиболее важным является вопрос о геометрических свойствах изображения, образовавшегося на сетчатке глаза, всюду будет приниматься простейшая модель, согласно которой на сетчатке в достаточно большом угле зрения двумерное изображение внешнего мира получается путем его проектирования при помощи хрусталика, выполняющего роль, аналогичную роли объектива фотоаппарата. Такое изображение на сетчатке глаза называют ретинальным изображением (от слова ретина - сетчатка глаза) или сетчаточным образом. Полезно еще раз подчеркнуть, что используемое здесь и ниже понятие "сетчаточный образ" является в достаточной мере условным: оно не учитывает фактической вогнутости поверхности сетчатки и подвижности глаза. Помимо того, сама сетчатка не является однородной - центральная (фовеальная) часть сетчатки дает наилучшее восприятие деталей и цветов, в то время как периферическая ее часть дает малую четкость восприятия. Следовательно, используемое в книге понятие "сетчаточный образ" является некоторой идеализацией, учитывающей совокупный эффект первой ступени зрительного восприятия. Сетчаточный образ дает сильно искаженную картину внешнего мира. Эти искажения прежде всего связаны с тем. что близкие предметы будут казаться огромными, а более удаленные - маленькими.
Ретинальное изображение само по себе не содержит никакой информации о расстояниях до предметов, образы которых возникли на сетчатке глаза. Поэтому соответствующее дополнение сетчаточного образа возможно путем привлечения какой-то другой информации. Этот процесс ввода дополнительной информации и является второй ступенью зрительного восприятия. Нужная информация извлекается из "запасов памяти" человеческого мозга. Несколько упрощая картину, можно утверждать, что человеческое сознание хранит в своей памяти опыт предшествующей жизни начиная с первых дней младенчества и даже генетически передаваемый опыт пред- шествующих поколений. Пользуясь этим опытом, человеческое сознание воссоздает по сетчаточному образу истинную картину внешнего мира с раз- умной степенью точности. Для последующего важно отметить, что образ внешнего мира, создаваемый мозгом, не является точной копией реального внешнего мира. Эта точность биологически бессмысленна и даже вредна - точным должно быть восприятие близких областей пространства, областей, могущих таить в себе опасность или могущих служить для добывания пищи, в то время как удаленные области можно и даже разумно воспринимать менее подробно и точно (чтобы не перегружать мозг излишней информацией, несущественной для определения поведения).
Эти "запасы памяти" являются не чем иным, как полученным в результате активной человеческой деятельности опытом, который позволяет с известным приближением правильно воспринимать окружающий человека объективный мир, давать хотя и приближенное, но адекватное отображение его, в сознании человека. Опыт познания внешнего мира, о котором здесь идет речь, не является суммой или итогом накопленной зрительной информации. Он включает всю совокупную человеческую практическую деятельность, которая позволяет корректировать представления человека о внешнем мире, коррелировать эти представления со зрительным восприятием и создавать, в конце концов, адекватный зрительный образ окружающего человека объективного мира с нужной степенью подробности и точности.
Воссоздаваемая мозгом по сетчаточному образу картина внешнего мира приобретает вид трехмерного пространства, но, как уже говорилось, иного по сравнений с реальным трехмерным, пространством. Поскольку художник в случае, когда целью его творчества является рисунок, а не чертеж, дол- жен уметь изображать именно зрительно воспринимаемое (перцептивное) пространство, его свойства следует рассмотреть более подробно. Если ограничиться только геометрией, то проблема сводится к вопросу о том, каким образом двумерное ретинальное изображение трансформируется в трехмерное перцептивное, точнее, каким геометрическим законам это преобразование подчиняется.
Прежде всего (не во времени, конечно, а логически) следует мысленно распределить все полученные на сетчатке изображения на соответствующие расстоянию от созерцающего их человека. Это распределение в направлениях "близко-далеко” происходит подсознательно, на основе предшествующего опыта, причем человек подсознательно пользуется рядом признаков глубины видимого пространства. Эти признаки можно условно разбить на две группы - монокулярные и бинокулярные. Первая группа характеризуется тем, что включенные в нее признаки глубины действуют и тогда, когда человек смотрит одним глазом.
К монокулярным признакам глубины можно отнести следующие:
1) перекрытие - более близкие предметы могут заслонять собой более далекие;
2) уменьшение размеров предметов по мере их удаления от зрителя; особенно эффективен этот признак, если рассматриваются предметы, истинный размер которых известен (деревья и т. п.);
3) явление воздушной перспективы - далекие предметы видны менее четко и меняют свой цвет (наблюдаются как бы через голубоватую дымку); 4) далекие предметы видны сдвинутыми вверх в поле зрения, точнее, приближенными к горизонту;
5) большие предметы (круглые крепостные башни, большие здания и т. п.), освещенные солнцем, оказываются затененными различным образом в различных своих частях, и наблюдаемая система теней способна дать представление о более близких и более далеких частях этих предметов; особенно эффективен этот признак для больших криволинейных и ребристых поверхностей.
Здесь перечислены не все монокулярные признаки глубины, но основные, причем те, которые будут нужны ниже.
К бинокулярным признакам глубины следует отнести:
1) конвергенцию - поворот оптических осей глаз в направлении рассматриваемого предмета, обычно (при взгляде вдаль) оптические оси глаз параллельны, однако если рассматривать достаточно близкий предмет, то соответствующие мышцы сводят оптические оси глаз так, чтобы они пересеклись в разглядываемой области пространства, и соответствующие мышечные усилия сигнализируют о близости или удаленности предмета;
2) диспаратность - даже если и не рассматривать какой-то предмет, то в силу того, что глаза разнесены, изображение, полученное левым и правым глазом, оказывается различным, причем тем более различным, чем ближе предметы к смотрящему.
Признаки глубины, действуя в совокупности, позволяют подучить достаточно полное представление о расстояниях до различных предметов причем по мере приближения к смотрящему число и "точность показаний признаков увеличиваются в полном соответствии с биологической потребностью человека. Если для больших расстояний нужная информация о дистанциях до предметов дается первыми четырьмя монокулярными признаками, то в непосредственной близости от человека действуют бинокулярные признаки и все монокулярные, за исключением лишь явления воздушной перспективы. Вдумчивое рассмотрение всех приведенных признаков глубины показывает, что они не могут быть непосредственно получены из сетчаточного образа, а рождены предшествующим опытом.
Даже такой, казалось бы, безусловный признак, как заслонение близких предметом далекого, не абсолютен, он предполагает знание истинной форм [2] частично заслоненного предмета, ибо иначе невозможно решить, являете .ли его видимая часть полной (а следовательно, не заслоненной) формой Таким образом, человеческий мозг, используя накопленный предшествующий опыт, дает принципиальную возможность построить по двумерном сетчаточному образу трехмерное перцептивное пространство.
Помимо подсознательного анализа зрительной информации, возникновению пространственного образа в сознании человека способствует информация (тоже извлекаемая из запасов памяти), никак не связанная со зрением. Находясь в привычном мире, человек не только созерцает его, но непрерывно взаимодействует с ним в своей практической деятельности: он перемещается, берет предметы в руки и т. п. Поэтому он прекрасно знает их размеры, форму своей комнаты, своего письменного стола, лежащих на нем предметов и вообще геометрические свойства окружающего его мира. То, что это знание может быть никак непосредственно не связанным со зрением (хотя весьма и помогающим ему), показывает практическая деятельность слепых. Слепой безошибочно находит нужные ему предметы в своей комнате, быстро и без посторонней помощи ходит по своей квартире и т. д. Это знание пространства, его размеров и формы можно назвать осязательно - кинестетичским представлением о нем, в частности позволяющим знать удаления в нем предметов от человека.
Хотя и в несколько иной форме, и возможно несколько ослаблено, это знание присуще и зрячему. В последнем нетрудно убедиться, разглядывая близкие предметы сначала двумя глазами, а затем закрыв один глаз. Казалось бы, "отключение” столь важных на малых расстояниях бинокулярны признаков глубины должно было бы вызвать существенное изменение зрительного восприятия. Однако ничего подобного не происходив человек продолжает видеть предметы в целом такими же и, главное, пространственными. Место бинокулярных признаков глубины в этом случае занимают осязательно-кинестетические представления. Таким образом, бинокулярные признаки глубины и осязательно-кинестетические представления выступают как бы в некотором единстве, способствуя правильной и точной оценки расстояний до предметов.
В том случае, когда искусственным образом у человека одновременно "отключались” оба названных источника информации, т. е. когда при наблюдении одним глазом из должным образом выбранной точки ему предъявлялись пространственные конструкции неизвестных ему и непривычных форм, оказалось возможным вызвать у человека зрительные иллюзии, совершенно искажающие фактические пространственные отношения. Об этом, в частности, говорят известные опыты с "перекошенной комнатой” Эймса Таким образом, признаки глубины, которыми способен пользоваться человек для "размещения” зафиксированных в сетчаточном образе предметов в направлении "близко-далеко”, сводятся к монокулярным и бинокулярным, дополненным осязательно-кинестетическими представлениями. Эффективность действия осязательно-кинестетических представлений, как и бинокулярных признаков глубины, падает с увеличением расстояния до созерцаемых предметов, если иметь в виду превышение расстояний, ограничивающих несколько неопределенную границу "непосредственного окружения” человека. Большие расстояния не столь важны биологически, и поэтому излишняя перегрузка памяти детальной информацией о больших областях пространства была бы биологически неразумна.
Возвращаясь к вопросу о формировании в человеческом сознании перцептивного пространства, отметим почти очевидное обстоятельство: одного "размещения” зарегистрированных сетчаткой глаза предметов по некоторой шкале расстояний недостаточно. Оптические процессы, связанные с работой глаза, дают на сетчатке явно искаженную картину внешнего мира - близкие предметы получаются большими, а далекие маленькими, даже если в объективном внешнем пространстве они совершенно одинаковы. С подобного рода искажением можно мириться для далеких областей пространства, однако для близких, имеющих первостепенную биологическую важность, всякого рода искажения крайне нежелательны, так как они могут привести к ошибкам поведения. Поэтому одной из задач системы зрительного восприятия является переработка в процессе второй ступени восприятия геометрических соотношений сетчаточного образа, причем эта переработка сильнее, чем ближе созерцаемая область пространства. Эти процессы "исправления” геометрии сетчаточного образа в настоящее время достаточно хорошо изучены и получили в психологии зрительного восприятия наименование механизмов константности. Остановимся на двух таких механизмах - механизме константности величины и механизме константности формы (другие механизмы константности, например константности цвета, как не имеющие геометрической природы, рассматриваться не будут).
Механизм константности величины связан с компенсацией уменьшения изображения некоторого предмета на сетчатке по мере его удаления. В зоне непосредственного окружения человека (т. е. в радиусе единиц метров) эта компенсация является почти полной. Следовательно, зрительный образ близкого предмета, возникающий в нашем сознании, может сильно отличаться по относительной величине от соответствующего ему сетчаточного образа, но зато будет согласован с истинной величиной созерцаемого предмета. В сказанном легко убедиться, рассматривая, например, пол в небольшой комнате. Действительно, наблюдая доски пола или паркетные полосы на расстоянии 3-4 м от себя и у своих ног, почти не ощущаешь их видимого ( См., например: ) сужения, в то время как на сетчатке глаза соответствующее сужение будет примерно двукратным (в согласии с отношением названного выше раccтояния к росту человека).
Таким образом, хотя по мере увеличения расстояния до объекта его величина на сетчатке уменьшается пропорционально расстоянию, воспринимаемая величина остается почти неизменной, константной (отсюда и название этого закона восприятия - механизм константности величины). Указанный факт хорошо известен художникам-портретистам. Создавая групповой портрет, художник пишет головы всех изображаемых приблизительно одинаковой величины, хотя на сетчатке глаза художника голова расположенного близко человека может быть много больше головы расположенного в глубине группы. Механизм константности величины не только увеличивает размеры удаленных предметов, но и уменьшает размеры слишком близких, например ладони, поднесенной к глазу. Как показали опыты, свойство константности величины оказывается почти абсолютным, настолько точно человеческое сознание воссоздает истинные размеры предметов по сетчаточному образу, если оно имеет информацию о расстояниях до них, однако при этом обнаружилось два фактора, которые неизменно снижали или полностью исключали действие механизма констант- ности величины:
1) константность нарушалась по отношению к далеким предметам;
2) константность не сохранялась и для близких предметов, если эти предметы имели мало или не имели вовсе признаков глубины
4. Оба эти экспериментальных факта полностью согласуются с нарисованной выше теоретической картиной - информация о далеких предметах имеет второстепенную биологическую ценность, а образование трехмерного перцептивного пространства возможно лишь при использовании признаков глубины, не содержащихся непосредственно в ретинальных изображениях. Механизм константности формы имеет аналогичную природу, однако касается формы предметов представим себе, что человек смотрит на пред- меты, имеющие простую форму - круга, квадрата и т. п. (например, по- верхности круглого или квадратного стола). Если смотреть на эти предметы под некоторым произвольным углом, то круг будет восприниматься как овал, квадрат - как фигура, похожая на ромб, и т. д. Действие механизма константности формы сказывается в том, что если человек заранее знает истинную форму созерцаемых предметов из своего предшествующего опыта, то круглые предметы кажутся ему не столь овальными, как их ретинальные изображения; углы ромбов оказываются более близкими к 90°, чем у их изо- бражений на сетчатке глаза (т. е. приближенными к квадрату), и т. д. Человеческое сознание стремится компенсировать не только искажения относительных размеров, но и искаженную форму предметов, возникающую при проектировании этих предметов на сетчатку при помощи оптической системы глаза. Хорошо известно, например, что экран телевизора можно наблюдать "сбоку” с большим отклонением от направления, перпендикулярного к плоскости экрана, и тем не менее видимая форма экрана будет сохраняться в виде вытянутого по горизонтали прямоугольника привычных очертаний, хотя на сетчатке его изображение уже может стать квадратным или даже вытянутым по вертикали. Механизм константности формы сравнительно легко изучить количественно, ставя опыты с предметами простой формы (круг, квадрат и т. п.), однако это не значит, что он не действует на сетчаточные изображения более сложных объектов.
Относительно эффективности механизма константности формы надо заметить следующее: 1) как уже говорилось, его действие тем сильнее, чем лучше известна {заранее, из предыдущего опыта) форма созерцаемого предмета;
2) он действует лишь на сравнительно малых расстояниях и совершенно .не эффективен для предметов, достаточно удаленных от смотрящего. Разумность обоих приведенных здесь условий с биологической точки зрения достаточно очевидна.
Возвращаясь к вопросу о двуступенчатом характере зрительного восприятия человека (в той степени подробности, которая нужна для последу- ющего), можно утверждать, что первой ступенью является образование на сетчатке изображения внешнего мира при помощи оптической системы глаза, а второй - воссоздание на этой основе трехмерного перцептивного про- странства с подсознательным использованием признаков глубины и осязательно-кинестетических представлений путем преобразования сетчаточного образа механизмами константности величины и формы. Последние как бы "растягивают” и "сжимают” отдельные элементы сетчаточного образа, подвергая наиболее существенным преобразованиям имеющую первостепенную биологическую важность часть сетчаточного образа, соответствующую области непосредственного окружения человека.
Сказанное здесь может создать излишне упрощенное представление о работе мозга при зрительном восприятии. Чтобы несколько уточнить характер работы мозга (опять лишь в той степени, в которой это будет нужно для последующего) и проиллюстрировать некоторые приводившиеся выше утверждения, обратимся к следующему примеру. На рис. b13-5 в средней части рисунка изображен куб, причем использована так называемая аксонометрическая проекция, при которой в изображении сохраняется свойство параллельности (ребра, параллельные у реального куба, изображены прямыми, которые между собой параллельны).

Приведенный рисунок замечателен в том отношении, что на нем изображены только ребра куба куб, изготовленный в виде проволочного каркаса) и поэтому перечисленные выше признаки глубины неэффективны. Действительно, бинокулярные признаки не способны содействовать правильности восприятия, поскольку глазам предъявлен не реальный куб, а его изображение. Более того бинокулярные признаки глубины при созерцании любого изображения объемного предмета на картине будут всегда только помехой, поскольку будут 'подчеркивать, что все точки изображения удалены от смотрящего на одно и то же расстояние, равное расстоянию от глаз до бумаги, холста или доски, и тем самым нарушать иллюзию изображения пространства (если художник ставил себе задачей передачу глубины пространства). Что касается монокулярных признаков глубины, то, создавая картину, художник способен опираться только на перечисленные выше монокулярные признаки глубины. Если обратиться к указанным пяти признакам, то легко убедиться, что все они в данном конкретном случае не могут дать необходимой мозгу информации; единственный признак, который мог бы оказаться полезным,- более удаленные предметы или их части видны при- ближенными к горизонту - не носит абсолютного характера. Приближение изображения предмета к линии горизонта может быть не только следствием удаления его от наблюдателя, но и следствием смещения в реальном про- странстве этого предмета или его части по вертикали. Сказанное иллюстрируется изображениями того же куба (b13-5Б, b13-5В), где показаны два возможных положения куба (b13-5А), которые конкретизировались, как только грани куба перестали быть прозрачными и вступил в действие абсолютный признак глубины - перекрытие (близкие предметы или их части заслоняют более далекие).